Model of Compton wavelength:
Assume the photon is incident along the X-axis. Then momentum conservation must exist in the Y-axis direction.
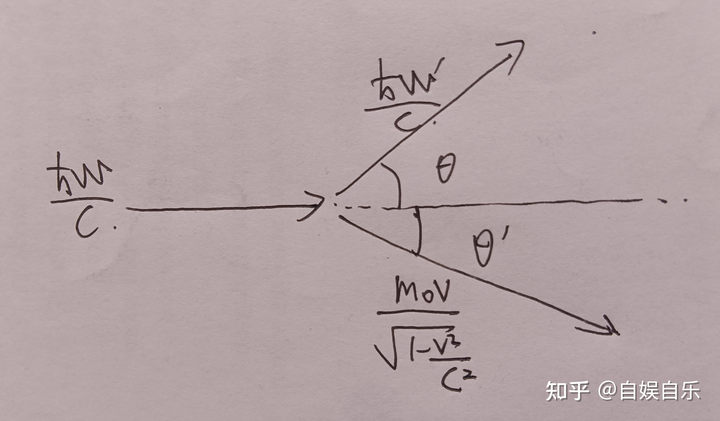
The upper is the laser beam output, and the lower is the electron output. According to the conservation law of momentum: \hbar \omega' /c \cdot sin \theta+ \gamma m_0 v \cdot sin \theta'=0.
(four variables here, including the electron speed v; The variables v and \theta actually cannot be directly related. But we will reduce it after).
The four-momentum of the photon before incidence is: P=(\hbar\omega/c,\hbar\omega/c,0,0) (1)
The four-momentum of the photon after incidence is: P'=(\hbar\omega'/c,\hbar\omega'\cdot\cos\theta/c,\hbar\omega'\cdot\sin\theta/c,0) (2)
The four-momentum of the electron before incidence is: P_e=(m_0c,0,0,0) (3)
The four-momentum of the electron after incidence is: P_e'=(\gamma m_0c,\gamma m_0v \cdot cos\theta',\gamma m_0v \cdot sin\theta',0) (4)
From the conservation of four-vectors we have: P+P_e=P'+P_e' \rightarrow P-P'=P_e'-P_e
Squaring gives: P²+P'^²-2PP'=P_e'^²+P_e²-2P_eP_e' (5)
In a high-energy environment, the photon’s energy is mainly contained in its momentum, so the photon mass can be ignored and the square of its four-momentum is zero: P²=P'^²=0 (6)
Substituting (1)(2)(3)(4)(6) into (5) yields: -\frac{2\hbar^2ωω'(1-cosθ)}{c²}=γ^2m_0^2c^2-γ^2m_0^2v^2+m_0^2c^2-2γm_0^2c^2 (7) (Where γ=\frac{1}{\sqrt{1-\frac{v²}{c²}}})
Because of conservation of energy, we also have: ℏω=ℏ\omega'+m_0c^2(γ-1)\rightarrow ℏ(ω-ω')=m_0c^2(γ-1) (8)
Dividing (8) by (7) gives (9): -\frac{ℏ(ω-ω')c²}{2ℏ²ωω'(1-cosθ)}=\frac{m_0c²(γ-1)}{γ²m_0²c²-γ²m_0²v²+m_0²c²-2γm_0²c²} (9)
Clearly, \frac{ω-ω'}{ωω'}=\frac{1}{ω'}-\frac{1}{ω}, and since ω=\frac{2πc}{λ},ω'=\frac{2πc}{λ'},
\frac{ω-ω'}{ωω'}=\frac{\lambda'-\lambda}{2\pi c}, and using the double-angle formula 1-cosθ=2sin^2 \frac{\theta}{2} Substituting into equation (9) and simplifying yields the modified Compton wavelength in a high-energy environment:
This expression looks very similar to the original formula, but now includes the variable v, which is exactly the speed we initially assumed for the electron after being scattered by the photon.
Note that
Reduce the variable v we got:
Result:
As stated above, the wavelength of the Relativistic Compton Scattering is:

Comment Section